Miko: Geisha 的半残编译器

人的命运就是这么不可预料，最后 Geisha 的编译器实现居然是作为学校的课程设计在考研期间抽空肝出来的。

因为各种因素，最后交上去的结果和预想的其实差了挺远——比如没来得及实现 GC 所以闭包是残缺的；比如自定义类型根本就没有。不过总归最后做成了一个有结果的东西（虽然是半残的）。

这篇是暑假期间作为课程报告交上去的文档。至于后续的工作，虽然现在已经考完研了但是突然又多出了一堆事情，只能看看什么时候有空能继续完善了……

代码当然也在 GitHub 上，只不过 star 都点在了之前那个 Haskell 写的前端 demo 上，这个就无人问津 emmmm

整体设计

利用了 rust-peg 生成语法分析程序，以 LLVM 为代码生成后端。

整体处理流程：

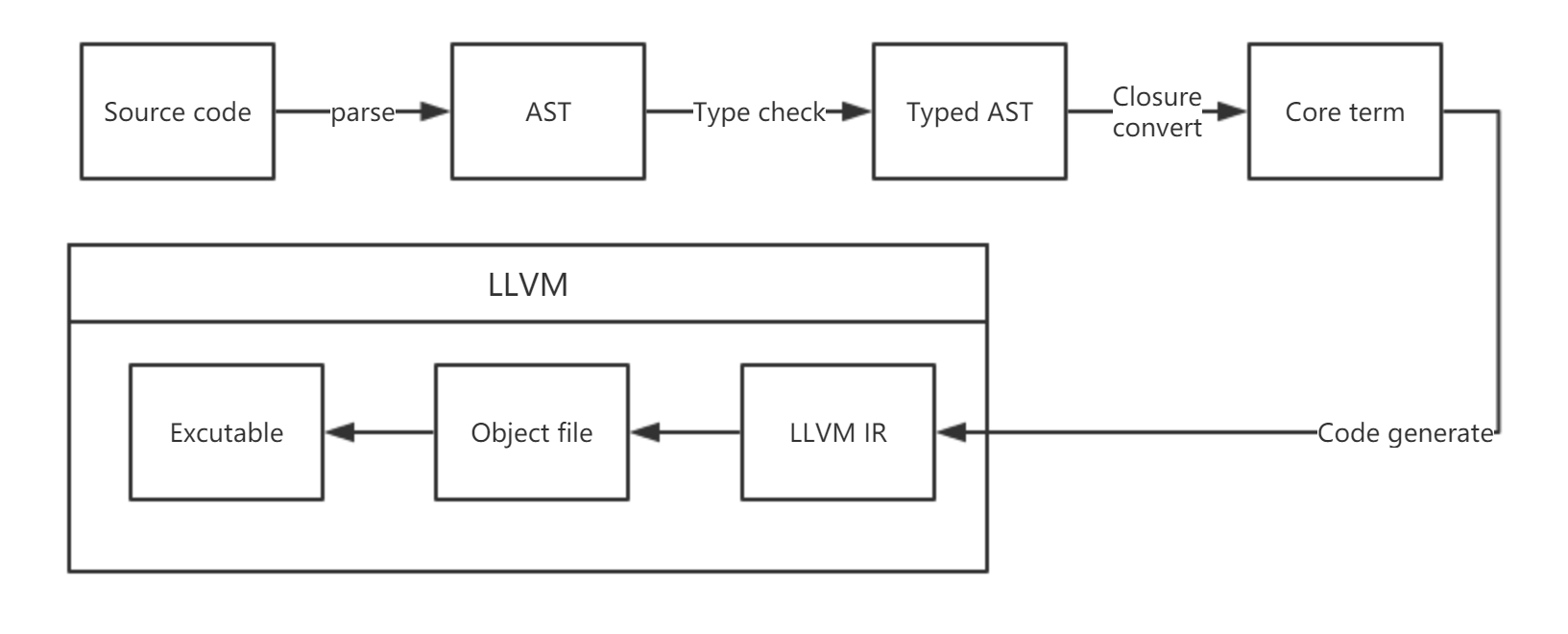
1505374261499

程序构建环境为 rust 最新 nightly 环境并依赖 LLVM 3.9。附件附带了 Windows x64 平台的可执行文件；链接过程需要执行 C 语言链接器。

命令行编译 input.gs 文件到 output.o 静态库文件命令为：

miko -o output.o input.gs

使用 clang/gcc 手动与 base.o 基础库链接生成可执行文件

cc -o output base.o output.o

语言定义

语言语义类似 OCaml 与 Haskell ，但是比 OCaml 更为严格，相较弱于 Haskell。

示例

全局函数定义与调用

def factorial(n) = if (n == 0) 1 else n * frac(n - 1)
def main() = putNumber(factorial(10))

输出 10!

变量绑定、闭包函数定义与调用

def main() =
    let n = 1 in
    let adder = (a) -> a + n in
    putNumber(adder(4))

输出 5

带类型注解的尾递归闭包函数定义

fib: Int -> Int
def fib(n) =
    let fib_tail = (n, p, c) ->
        if (n == 0)
            -1
        else if (n == 1)
            p
        else
            fib_tail(n - 1, c, p + c)
    in fib_tail(n, 0, 1)
main: Void -> Void
def main() =
    let f = fib(10) in
        putNumber(f)

输出 Fibonacci 数列第 10 项（从 1 开始计数）

文法定义

位于 CFG 文件（与当前实现有差异）。

类型系统

采用 HM 类型系统进行类型推导和类型检查。

（已经实现的部分）

基本类型
- Int
  
  32 位有符号整数
- Float
  
  64 位有符号 IEEE 浮点数
- Char
  
  8 位有符号整数（字符）
- String
  
  元素为 Char 的向量类型（暂未实现）
  
  暂时实现为静态字符数组常量
函数类型（arrow）

HM 函数类型

应用规则：
$\frac{\Gamma \vdash _D e_0 : \tau \to \tau' \; \Gamma \vdash _D e_1 : \tau}{\Gamma \vdash _D e_0(e_1) : \tau'}$
抽象规则：
$\frac{\Gamma,x : \tau \vdash _D e : \tau'}{\Gamma \vdash _D (x) \to e : \tau \to \tau'}$

积类型（production）

两个类型的积为一个新类型，其可能的取值范围为原来两类型的笛卡儿积。表现为多参数函数的参数类型或元组（tuple）。

（暂未实现部分）

泛型

基于具体化代码生成机制的泛型（类似 C++ 模板），并支持 concept 接口约束检查，进行静态接口多态分派。

当前编译器中只支持数值运算符的泛型。如 + 运算符的类型定义为 + : forall a . a * a -> a ，是一个对任何类型都可以应用的泛型函数（实际上只能用于 Int 和 Float 两种类型）。而实际上在支持 concept 接口约束的情况下，应该为 + : forall (Abelian a) . a * a -> a ，即作为内置接口 Abelian （阿贝尔群）的接口函数。
自定义类型（ADT）

关键字 data 定义一组枚举量，每个分支可附有具名或匿名字段，可附带泛型参数。如一个含有泛型 a 的类型 AbstractDataType 的定义：
data AbstractDataType a {
Variant1(a, Int),
Variant2 {
field1: a,
field2: String
},
Vartiant3
}
Concept（接口）

一个 concept 对于一个类型 a 给予一组函数定义，若一个类型 a’ 满足该 concept，则这组函数定义中的 a 类型必须全部满足 a 到 a’ 的替换。

值语义

用户不能直接接触内存，而是使用抽象的值。一旦将一个值绑定到特定名称上，在其作用域内不发生改变。绑定可以在子作用域内被暂时覆盖，但不能被取消。作用域结束后绑定失效。

函数闭包

函数定义时可以引用同作用域下的值（自由变量）。当一个函数被返回出它定义的作用域时，它所引用到的值的生存期将与其同步。

由于垃圾回收机制未完善，当前只支持同作用域下的函数闭包，而不支持返回引用了自由变量的函数闭包。

语法分析与抽象语法树

基于 rust-peg 生成 peg 语法分析器。位于 src/syntax/parser/grammar.rustpeg 。

顶层定义节点用 Def 表示，保存定义名、定义类型、位置等信息。

/// Represents a top level definition,
/// `def` or `data` or `type`
#[derive(Clone, PartialEq, Debug)]
pub struct Def {
    pub ident: Id,
    pub node: Item,
    pub pos: Span,
}
#[derive(Clone, PartialEq, Debug)]
pub enum Item {
    Form(E),
    Alias(Vec<Id>, P<Scheme>),
    Alg(Vec<Id>, Vec<Variant>),
}
#[derive(Clone, PartialEq, Eq, Hash, Debug, Copy)]
pub struct Span {
    start: usize,
    end: usize,
}

表达式（语法树）节点为 Form 。语法树 Form 中除了保存节点类型、名称、子节点外，还保存该节点对应源码的位置、类型约束。在完成类型推导之后还将保存类型结果。该定义位于 src/syntax/form.rs

/// Represents a form
#[derive(Clone, PartialEq,  Debug)]
pub struct Form {
    /// Expression content
    pub node: Expr,
    /// Form tag
    pub tag: FormTag,
}
#[derive(Clone, PartialEq, Eq, Hash, Debug)]
pub struct FormTag {
    /// Position in source
    pub pos: Span,
    /// Type of node
    pub ty: Scheme,
    /// Annotate type
    pub annotate: Option<Scheme>,
}
/// Represents a expression to be evalutated to a value
#[derive(Clone, PartialEq, Debug)]
pub enum Expr {
    /// Literial value
    Lit(Lit),
    /// Identifier (binding/definition)
    Var(Id),
    /// List (array)
    /// e.g. `[fuck, shit]`
    List(Vec<E>),
    /// Block (statement sequence)
    /// e.g. `{ print(fuck); print(shit); 1 }`
    Block(Vec<E>),
    /// Function apply
    /// `fuck(shit, 1)`
    Apply(E, Vec<E>),
    /// Abstruction (function)
    /// e.g. `(fuck, shit) -> fuck + shit`
    Abs(Lambda),
    /// Binary operator expression
    /// e.g. `fuck + shit`
    Binary(BinOp, E, E),
    /// Unary operator expression
    /// e.g. `!fuck`
    /// e.g. `-shit`
    Unary(UnOp, E),
    /// Let-in expression
    /// e.g. `let fuck = shit in fuck + 1`
    Let(VarDecl, E, E),
    /// Conditional expression
    /// e.g. `if (fuck == shit) 1 else 0`
    If(E, E, E),
}

其中 VarDecl 为名称与类型的组合，Lit 为字面量表示，两者为整个程序中的通用结构，位于 src/internal.rs

#[derive(Debug, PartialEq, Clone)]
pub struct VarDecl(pub Id, pub Scheme);
#[derive(Clone, PartialEq, Debug)]
pub enum Lit {
    Int(i32),
    Float(f64),
    Str(String),
    Bool(bool),
}

类型推导（类型检查）

表达式的类型分为两种：单态类型与多态类型（泛型），除此之外还有用于类型推导中表示未确定类型的 Slot ，定义位于 src/types.rs。多态类型在单态类型的基础上还保存了一个多态类型参数列表（泛型参数列表）。

/// Type scheme
#[derive(Clone, PartialEq, Eq, Hash, Debug)]
pub enum Scheme {
    /// A monomorphism type
    /// `Int * Int -> Double`
    Mono(Type),
    /// Polymorphism type
    /// `forall a. a * a -> a`
    Poly(Vec<Name>, Type),
    /// Unknown type
    Slot,
}

表达式的类型由六种基本类型组合成类型树，分别为 Void 表示无返回值、Var 泛型变量或未定类型、Con 确定的类型、Arr 函数类型、Prod 积类型、Comp 带参数的类型。

#[derive(Clone, PartialEq, Eq, Hash, Debug)]
pub enum Type {
    Void,
    /// Type variable
    Var(Name),
    /// Constant type name
    Con(Name),
    /// Arrow (->) type
    Arr(P<Type>, P<Type>),
    /// Product (*) type
    Prod(P<Type>, P<Type>),
    /// Composite type
    Comp(P<Type>, P<Type>),
}

类型推导的主要部分位于 src/typeinfer/infer.rs

类型推导的基本思想基于 Hindley–Milner 类型系统：

自底而上地把表达式的类型分为已知类型、多态类型、未知类型三种；
根据 HM 合一规则，把符合条件的未知类型约束为已知类型和多态类型；
如果发生冲突则报错，否则继续替换直到确定所有表达式的类型。

例如上例

def main() =
    let n = 1 in
    let adder = (a) -> a + n in
    putNumber(adder(4))

编译器内置的 + 运算符类型为 forall a. a * a -> a ，代表着两个参数和返回值需要是同一个类型，并且不限制它们的具体的类型。
表达式 (a) -> a + n 由于 + 的约束可以确定类型 m -> m ，其中 m 为待定类型；又由于 + 的约束，a 和 n 必须为同一类型，即 m。
由 let n = 1 ，1 确定为 Int 类型，故 n 确定为 Int 类型；故 m 类型即为 Int；故 adder 类型即为 Int -> Int 。
如此推断 adder(4) 为 Int 类型。又putNumber 为 Int -> Void 类型，参数类型相符；推断出 main 函数返回值为 Void 类型。

具体实现方面，使用了基于 constraint 的合一策略[1]，并在推导过程中追溯类型定义的位置用于报错信息。由于暂时没有实现泛型，类型推导出的非单态结果即使符合语义检查也将报错。

闭包转换

该部分位于 src/core/convert.rs。由于语言支持函数闭包——即嵌套的函数定义可以引用同级或上级作用域下的其它变量（自由变量），编译过程中需要找出每个函数所引用的所有自由变量，将其汇集成一个向量后作为函数的一个额外参数，之后将函数中所引用的自由变量对应到该额外参数的对应分量中。

即上例中的

def main() =
    let n = 1 in
    let adder = (a) -> a + n in
    putNumber(adder(4))

编译后的结果用类 C 语言表示即为

int adder(int a, void* fv)
{
  return (a + ((int *)fv)[0])
}
int main()
{
  int fv[] = {1};
  putNumber(adder(4, (void*)fv));
}

具体过程与这篇文章类似，自底向上归纳每个子节点的自由变量，最后得到整个函数的自由变量，将嵌套的函数定义全部展开为全局函数定义。

中间表示

闭包转换的结果是将 AST 转换为编译器的内部中间表示 core term。该中间表示较 AST 有几种不同的节点类型，并省去了不必要的信息。

其中全局定义的表示被具体定义为 FunDef 全局函数定义（类型定义尚未实现）。

#[derive(Clone, PartialEq, Debug)]
pub struct FunDef {
    name: Id,
    params: Vec<VarDecl>,
    freevars: Vec<VarDecl>,
    body: Node,
    ty: Scheme, 
}

表达式定义变为 TaggedTerm ，包含类型信息和真正的表达式 Term。

/// Represents a expression term
#[derive(Clone, PartialEq, Debug)]
pub struct TaggedTerm {
    ty: Scheme,
    node: Term,
}

Term 与 AST 相比，没有了 lambda 函数节点和函数调用 Apply 节点，取而代之的是生成闭包的 MakeCls 节点和表示闭包调用与直接调用两种调用形式的节点。

/// Represents a expression term
#[derive(Clone, PartialEq, Debug)]
pub enum Term {
    /// Literal value
    Lit(Lit),
    /// Identifier (binding/definition)
    Var(Id),
    /// List (array)
    /// e.g. `[fuck, shit]`
    List(Vec<Node>),
    /// Block (statement sequence)
    /// e.g. `{ print(fuck); print(shit); 1 }`
    Block(Vec<Node>),
    /// Make closure with free variables
    MakeCls(VarDecl, P<Closure>, Node),
    /// Apply a closure
    ApplyCls(Node, Vec<Node>),
    /// Apply function without free variables
    ApplyDir(VarDecl, Vec<Node>),
    /// Binary operator expression
    /// e.g. `fuck + shit`
    Binary(BinOp, Node, Node),
    /// Unary operator expression
    /// e.g. `!fuck`
    /// e.g. `-shit`
    Unary(UnOp, Node),
    /// Let-in expression
    /// e.g. `let fuck = shit in fuck + 1`
    Let(VarDecl, Node, Node),
    /// Conditional expression
    /// e.g. `if (fuck == shit) 1 else 0`
    If(Node, Node, Node),
}
/// Represents a closure, including a entry as
///   global definition and a actual free variable list.
#[derive(Clone, PartialEq, Debug)]
pub struct Closure {
    entry: Id,
    actualFv: Vec<Id>,
}

该部分位于 src/core/term.rs

代码生成

考虑到代码生成的质量和跨平台，使用 LLVM 作为代码生成目标。编译器使用 LLVM API 生成 LLVM IR 并转化为汇编代码或二进制库文件。代码生成模块主要位于 src/codegen/emit.rs 。

这里使用了 rust 版本的 LLVM 基础库 llvm-sys 并进行了额外封装，封装代码位于 libllvm/src 和 src/codegen/llvm.rs。

运行时

运行时调用的代码位于 src/lib 。编译器附带了一个供用户运行时调用的语言基础库（静态库 base.o），暂时只包含了示例代码中用到的输出函数。同时还有用于垃圾回收的库，不过由于时间紧迫并没有实装到编译过程中。

参考文献

[1] Generalizing Hindley-Milner Type Inference Algorithms

发布于 2018-01-06

tags:

{ programming language }

{ compiler }

{ rust }